News Gosip Rumors Celebrities Info

Most people find relative velocity to be a relatively difficult concept. In one dimension, however, it's reasonably straight-forward. Let's say you're walking along a road, heading west at 8 km/hr. A train track runs parallel to the road and a train is passing by, traveling at 40 km/hr west. There is also a car driving by on the road, going 30 km/hr east. How fast is the train traveling relative to you? How fast is the car traveling relative to you? And how fast is the train traveling relative to the car?

One way to look at it is this: in an hour, the train will be 40 km west of where you are now, but you will be 8 km west, so the train will be 32 km further west than you in an hour. Relative to you, then, the train has a velocity of 32 km/hr west. Similarly, relative to the train, you have a velocity of 32 km/hr east.

Using a subscript y for you, t for the train, and g for the ground, we can say this: the velocity of you relative to the ground = 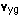 = 8 km/hr west the velocity of the train relative to the ground =  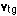= 40 km/hr west

Note that if you flip the order of the subscripts, to get the velocity of the ground relative to you, for example, you get an equal and opposite vector. You can write this equal and opposite vector by flipping the sign, or by reversing the direction, like this: the velocity of the ground relative to you = 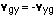 = -8 km/hr west = 8 km/hr east

The velocity of the train relative to you, 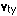 , can be found by adding vectors appropriately. Note the order of the subscripts in this equation: read more